Machine Learning is all the rage as companies try to make sense of the mountains of data they are collecting. Data is everywhere and proliferating at unprecedented speed. But, more data is not always better. In fact, large amounts of data can not only considerably slow down the system execution but can sometimes even produce worse performances in Data Analytics applications.
We have found, through years of formal and informal testing, that data dimensionality reduction — or the process of reducing the number of attributes under consideration when running analytics — is useful not only for speeding up algorithm execution but also for improving overall model performance. This doesn’t mean minimizing the volume of data being analyzed per se but rather being smarter about how data sets are constructed.
With the perpetual data crunching happening today, here’s a bit of an analytics refresher that could prove valuable in your operation.
The First Steps
When you consider a project, remember most Data Mining algorithms are columnwise implemented, which makes them slower and slower on a growing number of data columns. The first step then is to reduce the number of columns in the data set and lose the smallest amount of information possible at the same time.
To get started, here are some of the most commonly accepted techniques in the Data Analytics landscape that we have found to be effective:
• Missing Values Ratio. Data columns with too many missing values are unlikely to carry much useful information. Thus data columns with a percentage of missing values greater than a given threshold can be removed. The higher the threshold, the more aggressive the reduction.
• Low Variance Filter. Similarly, data columns with little changes in the values carry little information. Thus, all data columns with a variance lower than a given threshold can be removed. A word of caution: Variance is range dependent; therefore, normalization is required here before applying this technique.
• High Correlation Filter. Data columns with very similar trends are also likely to carry very similar information. In this case, only one of them will suffice to feed the Machine Learning model. Here we calculate the correlation coefficient between numerical columns and between nominal columns as the Pearson’s product-moment correlation coefficient and the Pearson’s chi square value, respectively. Pairs of columns with correlation coefficient higher than a threshold are reduced to only one. But, correlation is scale sensitive; therefore, data normalization is required for a meaningful correlation comparison.
The Fab Four
In addition to those simpler and somewhat intuitive techniques for column reduction, a number of other more complex techniques can assist with dimensionality reduction. While these techniques may seem more difficult, they are worth diving into for the integrity of your more sophisticated projects. I will explain four that we’ve found to be highly effective:
• Random Forests/Ensemble Trees. Decision tree ensembles, also referred to as random forests, are useful for feature selection in addition to being effective classifiers. One approach to dimensionality reduction is to generate a large and carefully constructed set of trees against a target attribute and then use each attribute’s usage statistics to find the most informative subset of features. Specifically, we can generate a large set (2,000) of very shallow trees (2 levels), with each tree being trained on a small fraction (3) of the total number of attributes. If an attribute is often selected as best split, it is most likely an informative feature to retain. A score calculated on the attribute usage statistics in the random forest tells us — relative to the other attributes — which are the most predictive attributes.
• Principal Component Analysis (PCA). Principal component analysis (PCA) is a statistical procedure that orthogonally transforms the original n coordinates of a data set into a new set of n coordinates called principal components. As a result of the transformation, the first principal component has the largest possible variance; each succeeding component has the highest possible variance under the constraint that it is orthogonal to (i.e., uncorrelated with) the preceding components. Keeping only the first m < n components reduces the data dimensionality while retaining most of the data information, i.e., the variation in the data. You should note that the PCA transformation is sensitive to the relative scaling of the original variables. Data column ranges need to be normalized before applying PCA. Also notice that the new coordinates (PCs) are not real system-produced variables anymore. Applying PCA to your data set loses its interpretability. If interpretability of the results is important for your analysis, PCA is not the transformation for your project.
• Backward Feature Elimination. In this technique, at a given iteration, the selected classification algorithm is trained on n input features. Then you remove one input feature at a time and train the same model on n-1 input features n times. The input feature whose removal has produced the smallest increase in the error rate is removed, leaving you with n-1input features. The classification is then repeated using n-2 features and so on. Each iteration k produces a model trained on n-k features and an error rate e(k). Selecting the maximum tolerable error rate, you can define the smallest number of features necessary to reach that classification performance with the selected Machine Learning algorithm.
• Forward Feature Construction. This is the inverse process to the backward feature elimination. Start with 1 feature only, progressively adding 1 feature at a time, i.e., the feature that produces the highest increase in performance. Both algorithms, backward feature elimination and forward feature construction, are quite time and computationally expensive. They are practically only applicable to a data set with an already relatively low number of input columns.
In Practice
Because this can get a bit in the weeds, it might be helpful to know how it all shakes out. We applied these techniques on large and slightly smaller data sets to see how they compared in terms of reduction ratio, degrading accuracy, and speed. It’s worth saying that the final accuracy and its degradation depend on the model selected for the analysis. Thus, the compromise between reduction ratio and final accuracy is optimized against a bag of three specific models: decision tree, neural networks, and Naive Bayes.
Running the optimization loop, the best cutoffs in terms of lowest number of columns and best accuracy were determined for each one of the seven dimensionality reduction techniques and for the best performing model. The final best model performance, as accuracy and area under the ROC Curve, was compared with the performance of the baseline algorithm using all input features.
We found that the highest reduction ratio without performance degradation is obtained by analyzing the decision cuts in random forests (random forests/ensemble trees). However, even just counting the number of missing values, measuring the column variance, and measuring the correlation of pairs of columns can lead to a satisfactory reduction rate while keeping performance unaltered with respect to the baseline models.
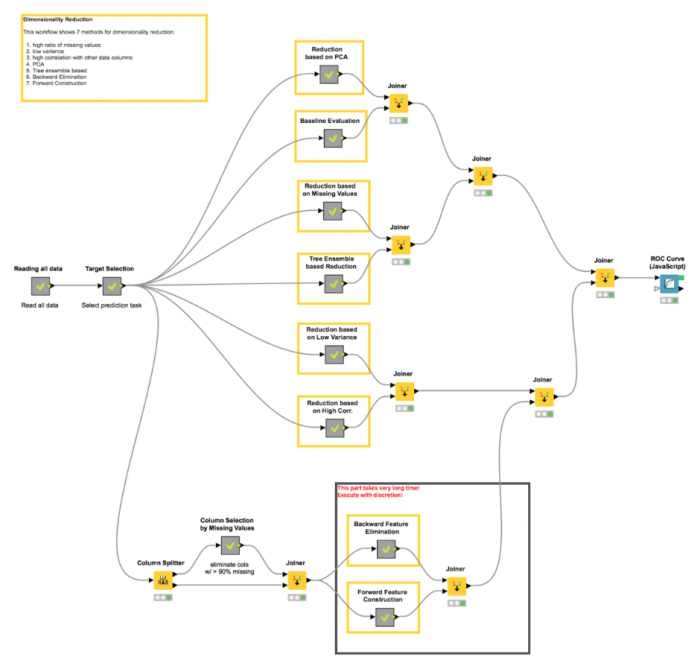
Image Credit: KNIME
In the era of Big Data, when more is axiomatically better, we have rediscovered that too many noisy or even faulty input data columns often lead to a less than desirable algorithm performance. Removing uninformative or even worse disinformative input attributes might help build a model on more extensive data regions, with more general classification rules, and overall with better performances on new unseen data.
This workflow can be downloaded from https://www.knime.com/nodeguide/analytics/preprocessing/techniques-for-dimensionality-reduction
or alternatively from the KNIME EXAMPLES public server at: 04_Analytics/01_Preprocessing/02_Techniques_for_Dimensionality_Reduction. If you want to know more about the KNIME EXAMPLES server, here is a video that might be useful: https://youtu.be/CRa_SbWgmVk.
As first published in Dataversity.



